What is a Factorial?
Before we dive into the specifics of 0 factorial, let’s quickly recap what a factorial is. In mathematics, the factorial of a non-negative integer n, denoted as n!, is the product of all positive integers less than or equal to n. For example:
- 1! = 1
- 2! = 2 × 1 = 2
- 3! = 3 × 2 × 1 = 6
- 4! = 4 × 3 × 2 × 1 = 24
The factorial operation is often used in combinatorics, probability theory, and other branches of mathematics to calculate the number of ways in which a set of objects can be arranged or selected.
The Definition of 0 Factorial
Now, let’s focus on the case of 0 factorial. By definition, 0! is equal to 1. This means that the product of all positive integers less than or equal to 0 is 1. At first glance, this may seem odd, as there are no positive integers less than or equal to 0. However, there are several compelling reasons why this definition holds true.
The Empty Product Rule
One of the primary reasons why 0! is defined as 1 is due to the empty product rule. In mathematics, an empty product is the result of multiplying no factors together. By convention, the empty product is always equal to 1. This rule is consistent with the multiplicative identity property, which states that multiplying any number by 1 yields the original number.
When we consider 0!, there are no factors to multiply, as there are no positive integers less than or equal to 0. Therefore, according to the empty product rule, 0! is equal to 1.
Consistency with the Recursive Definition
Another reason why 0! is defined as 1 is to maintain consistency with the recursive definition of the factorial function. The recursive definition states that for any positive integer n:
n! = n × (n-1)!
This means that the factorial of n is equal to n multiplied by the factorial of n-1. By extending this definition to include 0, we can see that:
1! = 1 × 0!
For this equation to hold true, 0! must be equal to 1. If 0! were defined as any other value, the recursive definition would break down, leading to inconsistencies in factorial calculations.
Combinatorial Interpretation
The definition of 0! as 1 also has a combinatorial interpretation. In combinatorics, n! represents the number of ways to arrange n distinct objects. When n = 0, we are essentially asking, “In how many ways can we arrange zero objects?”
The answer to this question is straightforward: there is only one way to arrange zero objects, which is to not arrange them at all. This single arrangement is represented by the empty set, and thus, 0! is equal to 1.
Implications and Applications
Now that we understand why 0! is defined as 1, let’s explore some of the implications and applications of this definition in various areas of mathematics.
Simplifying Expressions
The fact that 0! equals 1 can be used to simplify certain mathematical expressions. For example, consider the expression:
(n + 1)! ÷ n!
By plugging in n = 0, we get:
(0 + 1)! ÷ 0! = 1! ÷ 1 = 1
This simplification is only possible because 0! is defined as 1. If 0! were defined differently, the expression would yield a different result or might not be defined at all.
Binomial Coefficients
Binomial coefficients, often denoted as $\binom{n}{k}$, are used to calculate the number of ways to choose k objects from a set of n objects. The formula for binomial coefficients involves factorials:
$\binom{n}{k} = \frac{n!}{k!(n-k)!}$
When k = 0 or k = n, the binomial coefficient simplifies to 1. This is because:
$\binom{n}{0} = \frac{n!}{0!(n-0)!} = \frac{n!}{1 \cdot n!} = 1$
$\binom{n}{n} = \frac{n!}{n!(n-n)!} = \frac{n!}{n! \cdot 1} = 1$
These simplifications rely on the fact that 0! = 1. Without this definition, the binomial coefficients would not simplify correctly in these cases.
Taylor Series Expansions
In calculus, Taylor series expansions are used to approximate functions using polynomials. The general form of a Taylor series expansion around a point a is:
$f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!} (x-a)^n$
When evaluating the Taylor series expansion at the point a, the term corresponding to n = 0 simplifies to:
$\frac{f^{(0)}(a)}{0!} (x-a)^0 = \frac{f(a)}{1} \cdot 1 = f(a)$
This simplification is only possible because 0! is defined as 1. If 0! were defined differently, the Taylor series expansion would not evaluate correctly at the point a.

Frequently Asked Questions (FAQ)
-
Q: Why is it important to define 0! as 1?
A: Defining 0! as 1 maintains consistency with the recursive definition of the factorial function and ensures that various mathematical concepts, such as binomial coefficients and Taylor series expansions, work correctly. -
Q: What is the empty product rule?
A: The empty product rule states that the product of no factors is always equal to 1. This rule is consistent with the multiplicative identity property and is one of the reasons why 0! is defined as 1. -
Q: How does the definition of 0! as 1 relate to combinatorics?
A: In combinatorics, 0! represents the number of ways to arrange zero objects, which is only one way: to not arrange them at all. This single arrangement is represented by the empty set, and thus, 0! is equal to 1. -
Q: Can the definition of 0! as 1 be used to simplify mathematical expressions?
A: Yes, the fact that 0! equals 1 can be used to simplify certain expressions, such as (n + 1)! ÷ n! when n = 0. -
Q: What is the significance of 0! in Taylor series expansions?
A: In Taylor series expansions, the term corresponding to n = 0 involves 0! in the denominator. By defining 0! as 1, this term simplifies correctly to f(a), ensuring that the expansion evaluates correctly at the point a.
Conclusion
In conclusion, the definition of 0 factorial as 1 is not an arbitrary choice but a result of careful mathematical reasoning. It maintains consistency with the recursive definition of the factorial function, adheres to the empty product rule, and has a clear combinatorial interpretation. Moreover, this definition plays a crucial role in simplifying expressions, working with binomial coefficients, and evaluating Taylor series expansions.
By understanding the reasons behind why 0! equals 1, students and enthusiasts can better appreciate the elegance and interconnectedness of mathematical concepts. This knowledge will serve as a solid foundation for further exploration of advanced topics in algebra, combinatorics, and calculus.
As we conclude this in-depth article on 0 factorial, we hope that readers have gained a clear understanding of the concept and its significance in the world of mathematics. Embracing the beauty and logic behind this seemingly counterintuitive result will undoubtedly enhance one’s problem-solving skills and appreciation for the fascinating realm of numbers.
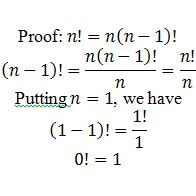
No responses yet